lesson 3.14.4 bubble sort

Implementing a Simple but Inefficient Sorting Algorithm

Imagine a cobbler who needs to sort a pile of shoes from smallest to largest size. There is a catch: the cobbler is blind (and yes, he has a terrible thumb). They cannot look at the line of shoes and instantly pick out the smallest. Instead, they have to pick up just two shoes at a time - one in the left hand, one in the right - and compare them by touch alone. If the left shoe feels longer than the right, they swap them over. This is exactly how a computer sorts data! It cannot "see" the whole list of data; it can only compare two specific values at a time. Today, we will learn the Bubble Sort, an algorithm that relies on these simple, blind comparisons to create perfect order from chaos.

Learning Outcomes

The Building Blocks (Factual Knowledge)

Recall that Bubble Sort works by repeatedly swapping adjacent elements if they are in the wrong order.

Describe the role of a temporary variable during a data swap to prevent data loss.

State that a "pass" constitutes one full journey through the list comparing pairs.

The Connections and Theories (Conceptual Knowledge)

Explain why the largest value is guaranteed to be in its correct final position after the first pass.

Analyse the pseudocode to identify how the algorithm reduces the search area (`n = n - 1`) after each pass.

Compare the "blind" nature of the computer's comparison (looking at only two items) to a human's ability to see the whole list.

The Skills and Methods (Procedural Outcomes)

Apply the logic of the "three-step swap" to exchange values in a list.

Create a robust Python implementation of Bubble Sort using a `while` loop and a `for` loop.

Evaluate the efficiency of the algorithm by observing how many passes are required to sort a random list.

Digital Skill Focus: Select, Copy and Paste code snippets accurately into the IDE, ensuring indentation is corrected if necessary.

Why do we sort?

In our previous lesson, we discovered the power of the Binary Search. It was incredibly fast, finding a needle in a haystack in just a few steps. But, it had one strict rule: the list must be sorted first.

If the data is jumbled (random order), we are stuck using the slower Linear Search. So, sorting is one of the most important jobs a computer performs. There are many ways to sort data, but today we start with the most famous one: the Bubble Sort.

The Blind Cobbler Analogy

Sorting is easy for humans because we can see the whole list at once. A computer is "blind" - it can only look at two specific values at any one time. To solve this, the Bubble Sort acts like our Blind Cobbler.

The Cobbler picks up the first two shoes.

They compare sizes.

If the shoe on the left is longer (bigger) than the shoe on the right, they swap them.

They move one step to the right and pick up the next pair.

By the time the Cobbler reaches the end of the line, the longest shoe has been swapped repeatedly until it reaches the very last spot. We say it has "bubbled" to the top. But, what about the rest of the shoes?

The science of swapping

You might think it's easy but think again...

The Mouse and the Elephant

Imagine we have two cages. Cage A has a Mouse. Cage B has an Elephant. We want to swap them so the Elephant is in A and the Mouse is in B. However, we have a problem - the elephant is terrified of the mouse so if we put them in the same cage, the elephant will panic.

How do we solve this? We need a third, empty cage called Transit.

Move Mouse (Cage A) to 'Transit'. (Cage A is now empty).

Move Elephant (Cage B) to Cage A. (Cage B is now empty).

Move Mouse ('Transit') to Cage B.

Swap complete with no panicky elephants!

The Bubble Sort Algorithm

Back to it. Let's write this logic down formally before coding it. To make it closer to real Python code, we can write the algorithm out in a closer version called pseudocode.

n = len(sequence)
swapped = true
while swapped = true
    swapped = false
    for i = 0 TO n-2
        if sequence[i] > sequence[i+1] then
           transit = sequence[i]
           sequence[i] = sequence[i+1]
           sequence[i+1] = transit
           swapped = true
        end if
    next i
    n = n - 1
end while

<< store the length of the sequence
<< make sure that the loop runs
<< keep going whilst 'swapped' = true
<< assume we haven't swapped
<< loop from the first item to the 'last'
<< if the left hand item is bigger than the right
<< store left hand item in transit
<< move the right hand item into the left hand one
<< move the transit value into the right hand item
<< record that we've swapped
<< end of selection
<< go back to the top of the loop
<< don't check the last item
<< end of while loop

Now, words, numbers and symbols are all well and good but a picture (or a gif) is worth a thousand words. Does this make it easier?

Task Code Construction

Let's build the Bubble Sort algorithm using Python.

Get Organised

Open up Thonny on your PC.

If it's the first time you've opened it today, you'll get a blank script otherwise click the new button to create a new one.

Organise your workspace.

Setup

Firstly, let's import the random library so we can use it's random number functions.

import random

Now, let's initialise the variables that we need to use during the sort. We'll set up a sequence of 16 random numbers between 0 and 99999, capture the length of the sequence and then set a 'flag' variable which we can use to track whether we've made any swaps. We assume we have to start with so the algorithm will start checking.

sequence = random.sample(range(100000),16)
n = len(sequence)
swap = True

What's the sitz?

It's always good to check where we are before we do anything.

print('Unordered :',sequence)

The sort logic

This is the big one. I've commented in the inner loop. Let's build this a bit at a time.

Loop as long as we haven't made any swaps. This is the outer loop:

while swap == True:

Let's assume we haven't done any swaps yet (because we haven't):

  swap = False

The inner loop. This is the loop that runs each pass through the list:

  for i in range(0,n-1):
    # is the left value bigger than the right?
    if sequence[i] > sequence[i+1]:
      # The 'elephant/mouse' swap
      temp = sequence[i]
      sequence[i] = sequence[i+1]
      sequence[i+1] = temp
      # We did a swap so we might not have finished yet...
      swap = True
  # We don't need to look at the last value in this pass because it's correct!
  n = n-1

Did it work?

Let's see if it worked or not...

print('Ordered   :',sequence)

PRIMM it!

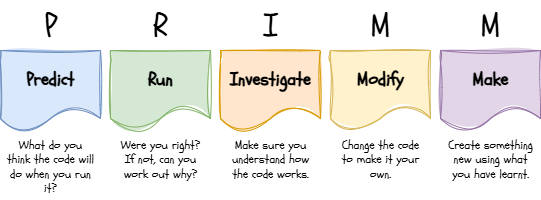
Predict what you'll see when you run the script.

Run the script. If you haven't saved it yet, it will ask you to before it will run - call it bubble-sort.py.

Predict: What happens if you remove the

n = n - 1

? Will it still sort? Will it be faster or slower?

Modify: Change the list size from 16 to 100 in the

random.sample

line. Does it make a difference to the length of time the script takes to run? What about trying 1000? 10000?

Make: Can you implement a comparisons check to see how much work the algorithm is doing? You'll need to add three extra lines to your script but I'm not going to tell you where...

Initialise the counter variable:

comparisons = 0

Increment the counter variable:

comparisons = comparisons + 1

Print the final value of the counter:

print(comparisons)

Outcome: A working, efficient Bubble Sort implementation.

Today you have learnt that sorting is achieved by blindly comparing pairs of items, swapping them if needed, and repeating this process until the data naturally "bubbles" into the correct order.