dijkstras shortest path algorithm
This page is about Dijkstra's shortest path algorithm
Algorithm
There are three main stages to most implementations of Dikjstra's shortest path algorithm and two main approaches. In this first approach, we use a table to trace the algorithm.

Set-up
Step 1. Create a trace table
1
Node
A list of all nodes in the graph
2
Visited
Indicates whether we have visited the node yet.
Initially blank because we haven't visited any nodes yet.
3
Shortest cost
Always holds the current value for the shortest cost to reach that node
4
Connections
A list of unvisited nodes reachable from that particular node along with the cost of reaching that node from the start node
Initially blank because we have started to explore any nodes
5
Order
Indicates the order in which the shortest cost is finalised
Should represent the order of nodes in increasing distance from the start node
Step 2. Complete the 'node' column
1
Write the names of the nodes
Mark the start node with a >
Mark the target node with a *
Step 3. Mark the start node as 'visited'
1
Put an 'x' in column (2) in the row containing the start node
Step 4. Initialise the 'shortest cost' column
1
Cost to reach start node = 0
We are already here
Embolden this cost to 'fix' it.
2
For all other nodes, the cost is ∞
We don't know if we can even reach them so we assume we can't.
Loop while there are still unvisited nodes
Step 5. Choose the unvisited node with the lowest cost
1
Look in column (3) for the node with the lowest cost
We will always explore node with lowest cost first
Initially, this is always the start node
2
If two or more unvisited nodes have the same cost, chose any.
Step 6. Mark the node as visited
1
Put a cross in column (2)
2
Optionally, cross through the node on the actual graph.
Step 7. Fix the most recent shortest cost for that node
1
Embolden the most recent cost in column (3)
2
This is the shortest distance to that node and can't be changed.
Step 8. Record the order
1
Add the incremental order in column (5)
The start node is always 1
Step 9. Update the cost for all reachable unvisited nodes
1
Calculate the cost of getting to that node
Write the name of the node you can reach followed by a colon in column (4)
Look at the cost of getting to current node and write this value
Add to this, the cost of getting to the reachable node
Calculate the cost of reaching the node
2
Update/relax the shortest cost
If the new cost to reach the node is less than the current shortest cost to reach the node:
Score through old shortest cost
Add new shortest cost in format Source node:cost
Otherwise, leave the current shortest cost
We've previously found a shorter route to reach the node
Report shortest cost to reach target node and work out route
Step 10. Return the shortest cost
1
Current shortest cost for target node.
Step 11. Work out path
1
Work back from target node
2
Follow the shortest costs back to start node
In the second approach, we redraw the graph using "labelling boxes" instead of nodes.
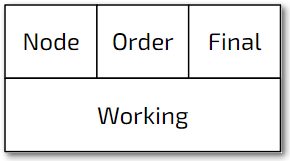
Set-up
Step 1. Redraw the graph with 'labelling boxes' instead of nodes
1
Node
is the name of the node
would normally appear in the circle
could be called 'vertex'
same as column 1 in the table version
2
Order
is the other in which the nodes are visited
could be called 'labelling order'
should follow increasing distance from the start node
corresponds to column 5 in table version
3
Final cost
will be the same as the most recent working value for that node
complete this when the node is visited
is the shortest distance of that node from the start node
could be called 'final label' or 'permanent label'
emboldened cost in column 3 in table version
4
Working values
helps keep track of the lowest cost;
corresponds to column 3 in the table version
Step 2. Initialise the final cost
1
The start node will have a final cost of 0
We are already at the start node.
2
For all other nodes, the final cost is blank
We have not calculated it yet.
Step 3. Initialise the working values
1
The start node has a working value of 0
We are already at the start node.
2
For all other nodes, the initial working value is ∞
We don't know if we can even reach them so we assume we can't
Loop while there are still unvisited nodes
Step 4. Choose the unvisited node with the lowest working value
1
Look in the labelling boxes for the node with the lowest working value
We will always explore node with lowest cost first
Initially, this will always be the start node.
2
If two or more unvisited nodes have the same cost, chose any.
Step 5. Fix the shortest cost for that node
1
Copy the most recent value in the 'working values' box into the 'final' value box.
2
This is the shortest distance to that node and can't be changed.
3
This essentially marks the node as 'visited'
Step 6. Record the order
1
Add the incremental order to the 'order' box
The start node is always 1
Step 7. Update the cost for all reachable unvisited nodes (have no 'final' value)
1
Calculate cost of getting to that node.
Add cost of getting to current node to the cost of the edge to reachable node.
optionally, score through the cost on the graph
2
Update/relax the shortest cost
If the new cost is lower than the more recent cost written in the 'working values' box:
Score through the previous shortest cost
Add the new shortest cost to the working values box. This becomes the new lowest cost to reach this node.
Otherwise, leave the current cost unaltered.
We've previously found a shorter route
Report shortest cost to reach target node and work out route
Step 8. Return the shortest cost
1
final value for the target node.
Step 9. Work out the path
1
Work from the target node
2
Two adjacent vertices lie on the shortest path if the difference between their final values is equal to the weight of the edge that connects them.
Implementation
This is an implementation of Dijkstra's Shortest Path Algorithm in C#.
using System;
namespace algorithms
{
public class Program
{
public static void Main()
{
int[,] graph = new int[,]
{
// 0 1 2 3 4 5 6 7 8
{ 0 , 4 , 0 , 0 , 0 , 0 , 0 , 8 , 0 }, // 0
{ 4 , 0 , 8 , 0 , 0 , 0 , 0 , 11, 0 }, // 1
{ 0 , 8 , 0 , 0 , 0 , 4 , 0 , 0 , 2 }, // 2
{ 0 , 0 , 7 , 0 , 9 , 14, 0 , 0 , 0 }, // 3
{ 0 , 0 , 0 , 9 , 0 , 10, 0 , 0 , 0 }, // 4
{ 0 , 0 , 4 , 14, 10, 0 , 2 , 0 , 0 }, // 5
{ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 1 , 6 }, // 6
{ 8 , 11, 0 , 0 , 0 , 0 , 1 , 0 , 7 }, // 7
{ 0 , 0 , 2 , 0 , 0 , 0 , 6 , 7 , 0 } // 8
};
Dijkstra dijk = new Dijkstra();
dijk.Calculate(graph, 4);
}
}
public class Dijkstra
{
public void Calculate(int[,] graph, int source)
{
int graphLength = graph.GetLength(0);
int[,] distance = new int[graphLength,2];
for (int i = 0; i < distance.GetLength(0); i++)
{
if (i == source)
{
distance[i,0] = 0;
}
else
{
distance[i,0] = int.MaxValue;
}
}
bool[] visited = new bool[graphLength];
visited[source] = true;
for (int i = 0; i < graphLength; i++)
{
int minIndex = GetMinDistance(distance, visited, source);
visited[minIndex] = true;
for (int j = 0; j < graphLength; j++)
{
if (!visited[j] && graph[minIndex,j] != 0 && distance[j,0] > distance[minIndex,0] + graph[minIndex,j])
{
distance[j,0] = distance[minIndex,0] + graph[minIndex,j];
distance[j,1] = minIndex;
}
}
}
PrintResults(distance,source);
}
private static int GetMinDistance(int[,] distance, bool[] visited, int source)
{
int minDistance = int.MaxValue;
int minIndex = source;
for (int i = 0; i < distance.GetLength(0); i++)
{
if (!visited[i] && distance[i,0] < minDistance)
{
minDistance = distance[i,0];
minIndex = i;
}
}
return minIndex;
}
private static void PrintResults(int[,] distance, int source)
{
Console.WriteLine("Vertex\tMin\tLast\tRoute");
for (int i = 0; i < distance.GetLength(0); i++)
{
List<string> route = new List<string>();
route.Add(i.ToString());
int nextNode = distance[i,1];
while (nextNode != 0) {
route.Add(nextNode.ToString());
nextNode = distance[nextNode,1];
};
if (route[route.ToArray().GetLength(0)-1] != source.ToString())
{
route.Add(source.ToString());
}
route.Reverse();
Console.WriteLine("{0}\t{1}\t{2}\t{3}", i, distance[i,0], distance[i,1],string.Join(">",route.ToArray()));
}
}
}
}Last modified: May 8th, 2024





















